当前位置： 论文资料 >> 理学论文 >> 地理地质 >> 地理空间的数学定义及定位型地图符号的制约因素分析
地理空间的数学定义及定位型地图符号的制约因素分析


　　定义2　 地球椭球面 存在地球椭球的长半径a和短半径b，若点集满足：
　　S=｛c|c=（x，y，z）∈DK∧ 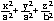=1｝　　　　 （2）
　　则称S为以a为长半径，b为短半径的地球椭球面，其中2b即地轴兼旋转轴[7]。
　　1.2 地理空间
　　地理科学研究的对象是地球的表层，具体地讲，上至同温层底部，下到岩石圈的上部，指陆地住下5～6公里，海洋往下4公里。设地球表层的上限为H1，下限为H2，从而得h的定义域（适用于“地球表层”概念）为h∈[-H2，H1]。根据h的取值，以h=0的椭球面为界面，可定义地球内空间和外空间。
　　定义3　 地球内空间 满足条件
　　IntK=｛P|P=（φ，λ，h）∈DL∧-H2≤h＜O｝ 　　（3）
　　的点集，称为地球内空间。
　　地球内空间即指岩石圈顶部至地球椭球面之间部分。由椭球面与真实地球表面之间的差异，因此存在虽在地表之上却因其处于椭球面内侧而属于地球内空间的点集。
　　定义4 　地球外空间 满足条件
　　ExtK=｛P|P=（φ，λ，h）∈DL∧O＜h≤H1｝　　　 （4）
　　的点集，称为地球外空间。
　　地球外空间即是地球椭球面到同温层底部的空间。由于椭球面与自然面之间的差异，同样存在虽在地表之下却因处于椭球面外侧而属地球外空间的点集。
　　定义5 　地理空间 地球内空间EntK、地球椭球面S和地球外空间EntK的并集，称为地理空间，即
　　K=EntK∪S∪ExtK|EntK，S，ExtK∈DL　　　　　 （5）
　　由于地理空间的上下限H1和-H2的选择与地球表层概念相适应，因此，地理空间的定义也就是地球表层的数学表述。
　　2 制图区域和制图物体
　　2.1 同胚
　　定义6 　同胚 设X和Y是两个随意的拓扑空间，并设f：X→Y。如果f是连续的双一一函数，并且它的反函数f -1也是连续的，那么，f就叫做空间X到空间Y上的同胚或拓扑映射或拓扑变换；此时空间X与空间Y叫做同胚的，记作X≈Y。
　　如果f是空间X到空间Y上的一个同胚，AX，并且B=f（A），则称点集A与点集B是同胚的，记作A≈B；此时又称点集B是点集A在同胚f之下的同胚象或拓扑象。如果f是空间X到空间Y上的一个同胚，g是空间Y到空间Z上的一个同胚，则复合函数gf是X到Z上的一个同胚。空间的同胚关系≈是一个等价关系[5]。地貌等高线图形，也就是其上覆地貌的同胚象[6]。
　　2.2 覆盖空间
　　定义7　 覆盖空间 设E和B是连通且局部道路连通的拓扑空间，f∶Ｅ→Ｂ是连续满射，如果对于每个c∈Ｂ，存在c的道路连通开域U，使得ｆ把ｆ -1（U）的每个通路连通分支同胚地映射成U，则称（E，ｆ）是Ｂ的覆盖空间，这种U称为容许邻域，Ｂ称为底空间，ｆ称为覆盖投影[10，11]。
　　2.3 制图区域和制图物体
　　2.3.1 椭球面上点c与过c点的椭球面法线ｈC的双一一函数关系
　　设c为椭球面Ｓ上的任意点，c∈S，过c点能且仅能作一条法线ｈC指向地理空间Ｋ。由于大地高ｈ以椭球面为起算面，故地球外空间ExtK=｛ｈC|0＜ｈC≤Ｈ1｝，地球内空间IntK=｛ｈC|-H2≤ｈC＜0｝。显然，地球空间的椭球面法线hC与椭球面上的投影点c是双一一函数。现把覆盖空间定义应用于地球外空间ExtK与地球椭球面S：令覆盖定义中的E=ExtK，B=S，f是连续满射，c∈S，|f -1（c）=hC∈ExtK，这里S是底空间，（f， ExtK）是S的覆盖空间，f为覆盖投影，c是hC在f下的同胚象或拓扑象。同理可说明地球内空间与地球椭球面的关系。
　　2.3.2 制图区域和制图物体的椭球面定位
　　定义8 　制图区域 设A为S的子集，AS，如果A是S中一个连通的开集，那末，A就叫做S中的一个区域。点c∈A，c的邻域U的原象f -1（U） ∈f -1（A）被作为制图对象时，则称f -1（U）为制图物体。f -1（A）在椭球面上的投影A称为制图区域。c的邻域U在球面上的外在特征有三种：
　　1） 当U=c为单一点时，称c为f -1（U）的点状定位；
　　2） 当U=lC，lC表现为线状连通集时，称lC为f -1（U）的线状定位；
　　3） 当U=SC，SC表现为面状连通集时，称SC为f -1（U）的面状定位。
　　地理空间中的物体f -1（U）在椭球面上的定位形式关联着它在地图平面上的定位形式并决定着其关联的地图符号的类型。

上一页  [1] [2]