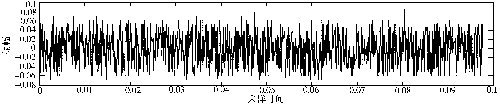
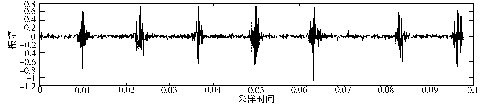
据统计,旋转机械的故障有30%是由轴承故障引起的。轴承振动信号携带了丰富的运行状态信息,当振动信号从平稳向非平稳过渡时,其突变往往反映了轴承故障引起的撞击、振荡、结构变化、间隙变化和断裂等。图1是对6310型轴承检测到的3种工况状态振动加速度的时域(以测取到的内环故障轴承信号中的最大值为分母对3种信号进行归一化处理)波形。从图中可见,正常轴承振动信号基本是平稳随机白噪声信号,而故障轴承振动信号则是非平稳随机有色噪声信号。
滚动轴承故障模式识别的任务就是对其振动信号中包含的状态信息进行提取和处理并加以分类,从而推断出滚动轴承运行的状态。由于滚动轴承系统的复杂性和故障形式的多样性,振动信号和状态信息之间并不存在确定的函数关系,信号集与状态集之间是一个复杂的非线性映射。这就决定了滚动轴承故障模式识别的难度和复杂性。
人工神经网络理论为描述这种映射关系提供了有效的工具。它通过对各种标准信号的处理和标准样本的学习,可以将处理和学习过程以权值和阈值模式集中存储和记忆在网络中,这样就可以通过网络的联想能力实现从信号空间到状态空间的非线性映射,从而达到模式识别的目的。
由于测得的轴承振动信号信噪比较低,笔者首先利用K-L(Karhuen-Loeve)变换将所测取的相关特征矢量X转换为独立的特征矢量Y以完成信号的特征矢量提取,然后利用提取的特征矢量的主特征值建立径向基函数神经网络,从而完成了基于K-L变换的时间序列空间到主特征矢量空间,基于径向基函数神经网络的主特征矢量空间到轴承故障空间的非线性映射,从而达到对滚动轴承故障状态进行模式识别的目的。
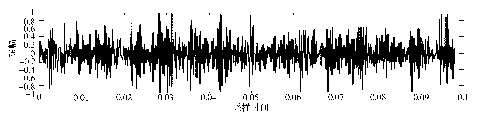
1 利用K-L变换提取主特征值[4,5,6]
设轴承振动信号可由n维模式向量X={xi}(i=1,2,…,n)描述 ,它对应原始空间中的一点,且存在一正交函数集A={Aj(i),i,j=1,2…,n}使得
Y=xjAj=AX1
其中变换后特征矢量Y=(y1,y2,…yn)T。式(1)的转置矩阵如下
YT=XTAT2
将式(1)与式(2)相乘并取数学期望可得
EYYT=AEXXTAT
Cy=ACx AT(3)
式中:Cx,Cy分别为X和Y的协方差矩阵,可利用
K-L线性变换方法适当选择变换矩阵A,使各分量yi间相互独立而使Cy成为对角矩阵,即
Cy=diag(λ1,λ2,…λn4
从而实现将相关特征矢量X变换成独立特征矢量Y进而完成主特征值(λ1,λ2,…λn分析的过程。
由于Cx是实对称矩阵,Cy是对角矩阵,它由Cx的n个正实特征根λ i i=12…n组成,且λ1>λ2>…>λn。根据协方差的概念,λii=12…n等于Y中的第i个分量的方差,从而λ i代表了振动信号的整体方差。
一般选择前面m个最大特征值对应的主特征矢量构成n维状态空间中的m维特征子空间,使
λλ>85%5
这时对应的m个矢量仍保留原信号的足够多的信息。也就是说,主特征值λi=12…m浓缩了原信号的主要信息,因而可以通过对轴承不同状态的主特征值的研究来达到故障模式识别的目的。
2 径向基函数(RBF)网络
径向基函数网络是以函数逼近理论为基础而构造的一类前向网络,这类网络的学习等价于在多维空间中寻找训练数据的最佳拟合平面。近年来的研究[7,8,9]表明,无论在逼近能力、分类能力(模式识别)和学习速度等方面均优于BP网络。
RBF网络的输出为
y=fx=WΦ‖x-ck‖26
由于Gaussian函数的良好性能,笔者采用Gaussian函数作为径向基函数。
Φx=exp7
由Gaussian核函数可看出,它具有两个矢量参数x和c,其中x是函数的自变量矢量,是输入,c是常数矢量,是径向基函数的中心。(x–c)构成了一个以c为中心的超椭圆,Φ(x - c)就是径向基函数。
径向基函数网络算法如下[7]:
Gaussian函数网络的学习参数有3个,即各RBF的中心ck、方差σk以及输出单元的权值Wk。
步骤1 从输入向量中选一组初始中心值ck ,注意ck 的值要不同。
步骤2 计算方差值:
σ=?穴8?雪
式中:dmax为最大的Eucilidean距离;K 为ck的数量。
步骤3初始化输出单位权。
步骤4由给定的输入x(n)计算输出(n):
in=WkΦck σk。
步骤5 更新RBF网络参数:
W(n+1)=W(n)+μWenΨn10
cn+1=cnμcΦ xn c σxn-cn
11
σn+1=σn+μΦ xncn σ‖xn-cn‖
12
式中:Ψn=en=in-ydnydn为网络期望输出;
μW,μc,μσ为3个参数的学习步长。
步骤6 如网络收敛,则计算停止;否则转到步骤4。
|